One-step equations are fundamental algebraic tools, often found in printable worksheets and online resources for grades 6-7․
These equations, like those involving adding or subtracting, build a crucial foundation for more complex mathematical concepts․
What are One-Step Equations?
One-step equations are algebraic equations that require only one operation to isolate the variable and solve for its value․ These equations typically involve basic arithmetic – addition, subtraction, multiplication, or division․
You’ll frequently encounter these when working through one-step equation worksheets (printable or online), designed for students in grades 6 and 7․
Essentially, they present a simple mathematical statement where the goal is to “undo” a single operation to find the unknown․ Examples include problems like y + 6 = 20 or 2n = 16, readily available for practice․
Why are One-Step Equations Important?
One-step equations serve as the building blocks for mastering more advanced algebraic concepts․ Proficiency with these foundational problems, often practiced using one-step equation worksheets, is crucial for success in higher-level math courses․
They develop essential problem-solving skills and reinforce the understanding of inverse operations․
Students in grades 6-7 benefit from consistent practice, as these skills are directly applicable to real-world scenarios and prepare them for tackling multi-step equations and beyond, solidifying their mathematical foundation․

Understanding the Core Principles
Core principles involve maintaining equality through operations, utilizing inverse actions – addition/subtraction, multiplication/division – to isolate variables, as shown in PDF examples․
The Equality Principle
The Equality Principle is the cornerstone of solving any equation, including simple one-step equations often practiced via PDF worksheets․ It states that any operation performed on one side of the equation must be mirrored on the other side to maintain balance․
Think of an equation as a perfectly balanced scale․ Adding or subtracting a weight from only one side will disrupt the balance․ Therefore, to isolate the variable and find its value, we manipulate the equation while consistently upholding this principle․ This ensures the equation remains true throughout the solving process, guaranteeing a correct solution․
Inverse Operations: The Key to Solving
Inverse operations are crucial for solving one-step equations, frequently practiced using PDF worksheets and online tutorials․ These operations “undo” each other – addition undoes subtraction, multiplication undoes division, and vice versa․
To isolate the variable, we employ the inverse of the operation currently acting upon it․ For example, if a variable is being added to, we subtract to neutralize it․ This maintains the equality principle, ensuring the equation remains balanced․ Mastering inverse operations is fundamental to successfully solving equations and building a strong algebraic foundation․

Solving Equations with Addition
Addition is used to isolate variables in equations, a skill reinforced through PDF practice problems and worksheets․ It’s a core concept for beginners!
Addition Property of Equality
The Addition Property of Equality states that adding the same number to both sides of an equation maintains the equality․ This principle is central to solving one-step equations, frequently demonstrated in PDF worksheets․
For instance, if you encounter an equation like ‘x ― 5 = 10’, you can add 5 to both sides․ This isolates ‘x’, revealing its value․
Numerous online resources and printable PDFs emphasize this property, providing students with ample practice․ Mastering this property is essential for building confidence and accuracy when tackling algebraic problems․
Example 1: Solving x ― 5 = 10
Let’s solve the equation x ― 5 = 10․ To isolate ‘x’, we apply the Addition Property of Equality, adding 5 to both sides․ This yields x ― 5 + 5 = 10 + 5, simplifying to x = 15․
Many PDF worksheets and online tutorials demonstrate this process step-by-step․ It’s crucial to remember that whatever operation is performed on one side of the equation must also be performed on the other․
Checking the solution is vital: 15 ― 5 = 10, confirming our answer․ Practice with similar examples found in PDF resources solidifies understanding․
Practice Problems: Addition
Test your understanding with these addition-based one-step equations! Solve for the variable in each problem․ Remember to utilize the Addition Property of Equality – adding the same value to both sides․
y ― 6 = 20 2) x ― 10 = 12 3) 12z ⎯ 15 = 3 4) 2n ⎯ 16 = 4 5) a ― 4 = 14 6) m ― 5 = 10․
Numerous PDF worksheets offer similar practice, alongside answer keys for self-assessment․ Consistent practice, using resources like these, builds confidence and fluency․ Check your solutions to ensure accuracy!
Solving Equations with Subtraction
Subtraction is a key inverse operation for solving one-step equations, readily practiced through PDF worksheets and online tutorials․
Subtraction Property of Equality
The Subtraction Property of Equality states that subtracting the same number from both sides of an equation maintains balance․ This principle is central to solving one-step equations involving addition․
Numerous PDF worksheets and online resources demonstrate this property with examples like y + 3 = 7․ To isolate ‘y’, we subtract 3 from both sides, resulting in y = 4․
This method ensures the equation remains valid while simplifying it to find the unknown variable’s value․ Mastering this property is vital for building algebraic proficiency, as evidenced by practice problems available online․
Example 2: Solving y + 3 = 7
Let’s solve the equation y + 3 = 7․ Our goal is to isolate ‘y’․ To do this, we apply the Subtraction Property of Equality․ We subtract 3 from both sides of the equation․
This gives us: y + 3 ⎯ 3 = 7 ⎯ 3, which simplifies to y = 4․ Many PDF worksheets illustrate this process step-by-step․
Always remember to check your solution! Substitute 4 back into the original equation: 4 + 3 = 7․ This confirms our answer is correct․ Practice with similar examples found in online tutorials reinforces this skill․
Practice Problems: Subtraction
Test your understanding with these subtraction-based one-step equations! Solutions and detailed steps are often available on PDF worksheets and online resources․
Solve for the variable in each equation: 1) x + 5 = 12, 2) a + 8 = 15, 3) m + 2 = 9, 4) b + 7 = 11, 5) z + 1 = 6․
Remember to use the Subtraction Property of Equality – subtract the constant term from both sides to isolate the variable․ Check your answers by substituting them back into the original equation․ Consistent practice, using printable worksheets, builds confidence!
Solving Equations with Multiplication
Multiplication is used to isolate variables in equations like z / 2 = 4, often practiced with PDF worksheets․
These problems reinforce the Multiplication Property of Equality for effective problem-solving․
Multiplication Property of Equality
The Multiplication Property of Equality states that you can multiply both sides of an equation by the same non-zero number without changing the equation’s balance․ This principle is vital when solving one-step equations where the variable is being divided by a number․
For instance, if you encounter an equation like x / 5 = 3, you’d multiply both sides by 5 to isolate ‘x’․ Many PDF worksheets and online tutorials demonstrate this, providing ample practice․ Understanding this property is key to successfully manipulating equations and finding the value of the unknown variable, building a strong algebraic foundation․
Example 3: Solving z / 2 = 4
Let’s solve the equation z / 2 = 4․ To isolate ‘z’, we apply the Multiplication Property of Equality․ This means multiplying both sides of the equation by 2․
(z / 2) * 2 = 4 * 2․ This simplifies to z = 8․ Numerous PDF worksheets and online resources demonstrate this step-by-step; Always remember to perform the same operation on both sides to maintain equality․ Checking your answer is crucial: 8 / 2 = 4, confirming our solution․ Mastering this process is fundamental for tackling more complex algebraic problems․
Practice Problems: Multiplication
Test your understanding with these practice problems! Remember to use the Multiplication Property of Equality to isolate the variable․
x / 5 = 7 2) y / 3 = 9 3) 10a / 2 = 5 4) b / 4 = 6․ Solutions and step-by-step explanations are often available in PDF worksheets and online tutorials․
Ensure you multiply both sides of the equation by the denominator to solve for the unknown variable․ Checking your answers is vital for accuracy․ Consistent practice using these resources will solidify your skills in solving one-step multiplication equations․
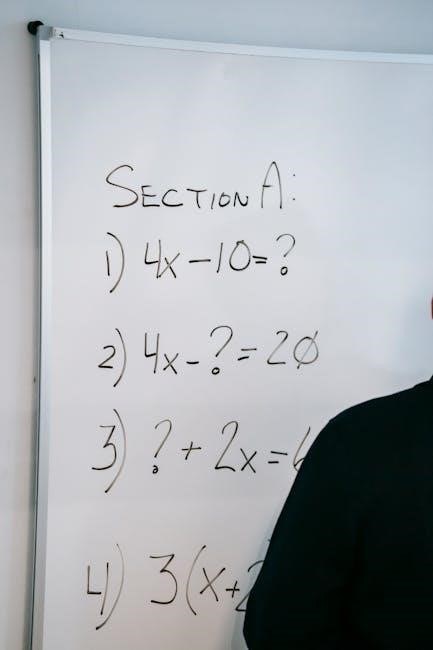
Solving Equations with Division
Division is used to isolate variables when they are being multiplied, often demonstrated in PDF worksheets and tutorials for easy practice․
Division Property of Equality
The Division Property of Equality states that you can divide both sides of an equation by the same non-zero number without changing the equation’s balance․ This principle is key when a variable is multiplied by a constant․
Many one-step equations PDF worksheets and online resources emphasize this property, providing examples like solving 3a = 15 by dividing both sides by 3, resulting in a = 5․
Understanding this property, alongside inverse operations, is crucial for successfully isolating the variable and finding its value․ Practice with downloadable worksheets reinforces this skill․
Example 4: Solving 3a = 15
Let’s solve the equation 3a = 15․ To isolate ‘a’, we need to undo the multiplication․ Remember, the goal is to get ‘a’ by itself!
Applying the Division Property of Equality, we divide both sides of the equation by 3․ This gives us (3a)/3 = 15/3․
Simplifying, we get a = 5․ Many one-step equations PDF resources demonstrate this process․ Always check your answer by substituting 5 back into the original equation: 3 * 5 = 15, which is true!
Practice Problems: Division
Test your understanding of solving one-step equations using division! Remember to apply the Division Property of Equality to both sides․
- 4x = 28
- y / 7 = 3
- 10z = 50
- b / 2 = 9
- 6a = 36
- c / 5 = 6
You can find solutions and more practice within one-step equations PDF worksheets available online․ Don’t forget to check your answers by substituting them back into the original equations to verify their correctness!

Working with Negative Numbers
One-step equations PDF resources often include problems with negative numbers, requiring careful attention to addition and subtraction rules․
Adding and Subtracting Negative Numbers in Equations
One-step equations PDF worksheets frequently test understanding of negative number operations․ Remember that subtracting a negative number is equivalent to adding its positive counterpart – a common source of errors!
For example, solving x ― (-2) = 5 requires recognizing that ― (-2) becomes +2, transforming the equation to x + 2 = 5․
Practice with these types of problems is essential․ Resources emphasize mastering these rules before tackling more complex algebraic manipulations․ Consistent practice builds confidence and accuracy when dealing with negative values within equations․
Example 5: Solving x ― (-2) = 5
Let’s solve x ⎯ (-2) = 5․ Remember, subtracting a negative is the same as adding a positive․ This transforms the equation into x + 2 = 5․
To isolate x, we need to perform the inverse operation of addition, which is subtraction․ We subtract 2 from both sides of the equation, maintaining balance․
This gives us x + 2 ― 2 = 5 ― 2, simplifying to x = 3․ Many one-step equations PDF worksheets include similar examples for practice․ Always check your solution by substituting 3 back into the original equation!
Practice Problems: Negative Numbers
Test your understanding with these problems involving negative numbers! Remember to utilize inverse operations to isolate the variable․
y + (-8) = 2 2) z ⎯ (-5) = 11 3) 3 + a = -1 4) b ― 7 = -3 5) -4 + c = 6․
These problems, commonly found in one-step equations PDF worksheets, reinforce the rules of adding and subtracting with negative integers․
Show your work and check your answers to ensure accuracy․ Consistent practice is key to mastering these foundational algebraic skills!

Checking Your Solutions
Verification is vital! Substitute your answer back into the original equation to confirm its validity, as shown in one-step equations PDF guides․
The Importance of Verification
Why check your work? Even with careful calculations, errors can occur when solving one-step equations․ Verification ensures accuracy and solidifies understanding․ Many one-step equations PDF resources emphasize this crucial step․
Substituting your solution back into the original equation acts as a self-check․ If both sides of the equation are equal, your answer is correct! This process isn’t just about finding the right number; it’s about developing a habit of mathematical precision and building confidence in your problem-solving abilities․ Don’t skip this vital step!
How to Check Your Answer
Checking is simple! Take the value you found for the variable and substitute it back into the original one-step equation․ For example, if you solved x ― 6 = 2 and found x = 8, replace ‘x’ with ‘8’․
This gives you 8 ⎯ 6 = 2․ Simplify the equation․ If both sides are equal (2 = 2), your solution is correct! Many one-step equations PDF worksheets include space for this verification step․ Practicing this consistently reinforces accuracy and builds confidence in your algebraic skills․ It’s a powerful habit!

Real-World Applications
One-step equations appear in everyday scenarios, often presented as word problems․ Printable one-step equations PDF resources help students translate these situations into solvable equations․
Word Problems Involving One-Step Equations
One-step equation word problems bridge the gap between abstract algebra and practical applications․ Many one-step equations PDF worksheets dedicate sections to these scenarios, fostering problem-solving skills․
For example, a problem might state: “Sarah had some apples, and she gave 5 away․ She now has 12 apples․ How many did she start with?” This translates to x ⎯ 5 = 12․
These problems require students to identify the unknown, translate the words into an equation, and then solve using inverse operations․ Mastering this skill is vital for future mathematical success, and readily available resources aid comprehension․
Example 6: A Word Problem Solution
Let’s revisit the apple problem: “Sarah had some apples, and she gave 5 away․ She now has 12 apples․ How many did she start with?” This translates to x ― 5 = 12․
To solve, we apply the addition property of equality, adding 5 to both sides: x ― 5 + 5 = 12 + 5․ This simplifies to x = 17․
Therefore, Sarah initially had 17 apples․ Many one-step equations PDF resources demonstrate this process step-by-step, reinforcing the concept․ Always check your answer: 17 ― 5 = 12․ This confirms our solution is correct․
Common Mistakes to Avoid
Students often incorrectly apply inverse operations or forget to perform the same operation on both sides of the equation, as shown in one-step equations PDF guides․
Incorrectly Applying Inverse Operations
A frequent error when solving one-step equations PDF problems involves misapplying the inverse operation․ For instance, if the equation is x + 5 = 12, students might incorrectly add 5 to both sides instead of subtracting․
Remember, the goal is to isolate the variable․ Therefore, using the opposite operation – subtraction in this case – is crucial․ Carefully reviewing one-step equations PDF examples can reinforce this concept․
Always double-check that the operation you’re performing will move you closer to having the variable alone on one side of the equation․
Forgetting the Equality Sign
A surprisingly common mistake when working with one-step equations PDF exercises is omitting the equality sign during the solution process․ An equation must maintain its balance; any operation performed on one side requires the identical operation on the other․
For example, solving x ― 3 = 7 often results in students writing “x = 10” without showing the intermediate step “x ― 3 + 3 = 7 + 3”․
Always consciously rewrite the entire equation after each step to avoid this error, ensuring the equality is preserved throughout․

Resources for Further Practice
Numerous one-step equations PDF worksheets, online tutorials, and examples are readily available to reinforce learning and build confidence in solving equations․
Online Worksheets and Tutorials
Numerous websites offer interactive online worksheets specifically designed for practicing one-step equations․ These resources often provide immediate feedback, helping students identify and correct errors in real-time․
Many platforms categorize problems by operation – addition, subtraction, multiplication, and division – allowing focused practice․
Khan Academy and Math-Drills․com are excellent starting points, providing comprehensive tutorials and a vast library of printable and digital worksheets․
Searching for “one-step equations practice” yields a wealth of options, including those formatted as PDF documents for convenient offline access and printing․
PDF Worksheets for Download
PDF worksheets offer a convenient, offline method for practicing one-step equations․ These downloadable resources are readily available from various educational websites, providing a structured approach to skill development․
Math-Drills․com, for example, hosts a comprehensive collection of PDF worksheets categorized by difficulty and operation type․
These worksheets typically include answer keys, enabling self-assessment and independent learning․
The advantage of PDF format lies in its portability and printability, making it ideal for classroom use, homework assignments, or supplemental practice, reinforcing concepts learned through online tutorials․

Advanced Concepts (Brief Overview)
Building upon one-step equations, students progress to two-step equations and those requiring combining like terms before isolation, expanding algebraic proficiency․
Two-Step Equations ― A Stepping Stone
Transitioning from mastering one-step equations, students encounter two-step equations, representing a logical progression in algebraic problem-solving․ These equations necessitate applying inverse operations in a specific sequence – typically undoing addition or subtraction before addressing multiplication or division․
This builds upon the core principles established with simpler equations, reinforcing the equality principle and the strategic use of inverse operations․ Printable worksheets and online tutorials often present these as a natural extension, preparing students for even more complex algebraic manipulations․
Successfully navigating two-step equations solidifies a student’s understanding of equation solving fundamentals․
Combining Like Terms Before Solving
Before directly applying inverse operations, some equations require a preliminary step: combining like terms․ This simplification process involves merging terms that share the same variable and exponent, streamlining the equation before isolation begins․
Worksheets and online resources emphasize this skill, often presenting equations where combining terms – like 3x + 2x – results in a simpler equation (5x)․ This prepares students for more complex scenarios․
Mastering this technique enhances efficiency and reduces the potential for errors in subsequent steps, building a stronger foundation in algebraic manipulation․
One-step equations are a vital starting point for algebra, readily practiced through downloadable PDF worksheets and online tutorials․
They form the basis for tackling increasingly complex mathematical problems․
Recap of Key Concepts
One-step equations, frequently practiced using PDF worksheets, center around isolating the variable using inverse operations․ Remember the equality principle: whatever operation is performed on one side must be mirrored on the other․
Addition and subtraction are inverses, as are multiplication and division․ Solving involves applying the correct inverse operation to ‘undo’ what’s being done to the variable․
Verification is crucial – substitute your solution back into the original equation to confirm its accuracy․ Mastering these foundational skills, available through numerous online resources, prepares students for more advanced algebraic concepts․
The Foundation for More Complex Equations
One-step equations, readily available as PDF practice materials, aren’t just isolated skills; they’re the bedrock for tackling multi-step problems․ Understanding how to isolate a variable with a single operation builds confidence and procedural fluency․
This foundational knowledge extends to solving inequalities, systems of equations, and eventually, more advanced algebraic manipulations․
Successfully navigating one-step equations, often reinforced through worksheets and tutorials, establishes a strong conceptual understanding essential for future mathematical success and problem-solving abilities․